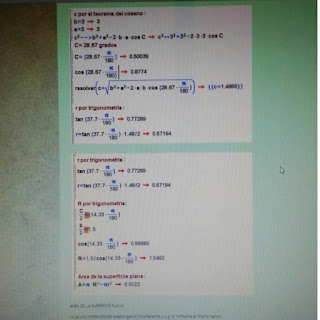
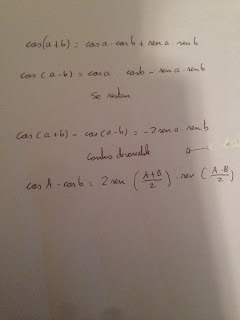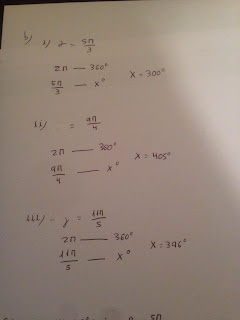¿POR QUÉ SE SINCRONIZAN LOS METRÓNOMOS?

http://naukas.com/2013/05/22/por-que-se-sincronizan-los-metronomos

Vamos a reflexionar sobre este vídeo y esta página: 

Es increíble ver como todos los metrónomos al principio estaban muy descoordinados pero ha medida que avanza el tiempo empiezan a sincronizarse.

La reflexión que creo que mi profesor quiere que llevemos este fenómeno a como  organizamos en clase.

Yo creo que también lo que quiere dar a entender nuestro profesor es que si uno trabaja muy bien podemos vernos reflejamos en ella o en él y que si uno lo puede hacer los demás también lo podemos hacer.

Pero sobre mi puto de vista a veces es así pero otras no; porque hay gente que tiene más facilidad de aprender y a otras personas les cuesta más entenderlo por eso yo pienso y reflexiono que hay que ayudarnos unos a otros y vernos reflejamos en gente que lo entienda pero también yo pienso que no todo es así de fácil. 

Y que deberíamos llegar a un acuerdo entre profesor y alumnos y así todo sería más fácil.

EXAMEN PARA CASA

Ejercicio 1:

Incentro de un triángulo: es el punto de intersección de 2 ángulos interiores cualesquiera de dicho triángulo, por ejemplo A y B.

He utilizado el GEOGEBRA para dibujar este triángulo.

No es una corono circular porque sus circunferencias no son concéntricas.

Ahora he resuelto con WIRIS el área de la región plana comprendida entre la circunferencia inscrita y la circunferencia circunscrita,

Ejercicio 2

He dibujado la ubicación, las dimensiones del claustro y del pozo con el GEOGEBRA.

 Y para calcular las dimensiones del claustro que se desconocen he hecho los cálculos mediante WIRIS.

Ejercicio 3: 

A) La construcción con GEOGEBRA.

B)

C) Son semejantes porque si aumento la altura, la base disminuye y si la base aumenta, la altura disminuye.

Ejercicio 4:

Primero dibujamos en GEOGEBRA la figura:

Y ahora resolvemos el triángulo por medio de WIRIS

TRANSFORMACIONES DE SUMAS DE DOS RAZONES EN PRODUCTOS.

TRANSFORMACIÓN DE LA SUMA DE SENOS EN PRODUCTOS:

 Siempre se parte de 2 fórmulas; después las sumaríamos y por último haríamos un cambio de variable y obtendríamos la fórmula definitva.

TRANSFORMACIÓN DE LA DIFERENCIA DE SENOS EN PRODUCTOS:

Se partiría de las dos fórmula de arriba pero en vez de sumarlas se restarían después se haría en mismo cambio de variable y obtendríamos la fórmula definitiva.

TRANSFORMACIÓN DE LA SUMA DE DOS COSENOS EN PRODUCTOS: 

Siempre se partiría de 2 fórmula después de sumarían, se haría un cambio de variable y después se obtendría la fórmula final.

TRANSFORMACIONES DE LA DIFERENCIA DE DOS COSENOS EN PRODUCTOS: 

Se partiría de las dos fórmulas de arriba pero en vez de sumarlas, restarlas; después se haría el mismo cambio de variable y se obtendría la fórmula.

EJERCICIOS TEMA 4

Ejercicio 1

Ejercicio 2

Ejercicio 3

Ejercicio 4

Ejercicio 5

Ejercicio 6

Ejercicio 7

Ejercicio 8

RAZONES TRIGONOMÉTRICAS DEL ÁNGULO DOBLE

Para obtener estas razones de ángulo doble se parte de las razones anteriores; entonces tas serían las fórmulas.

TEOREMAS DE ADICIÓN

Seno de la suma y diferencia de los 2 ángulos:

Sen( A+ B) = Sen A+ Sen B; esto no es correcto; porque Sen 90 grados = Sen ( 45º + 45º ) = raíz de 2 entre dos mas raíz de 2 entre 2 = raíz de dos y eso no es verdad en realidad seria 1.

Lo correcto sería....

Coseno de la suma y de la diferencia  de dos ángulos:

Tangente de la suma y de la diferencia de dos ángulos:

FILÓSOFOS MATEMÁTICOS ASTRÓNOMOS GRIEGOS

MAPA

PROPOSICIÓN CON DEMOSTRACIÓN

Estábamos en clase corrigiendo los exámenes por grupos que hicimos hace 2 o 3 semanas; y a partir de esa corrección el profesor nos propuso una proposición muy interesante:

PROPOSICIÓN:

DEMOSTRACIÓN:

RESOLUCIÓN DE TRIÁNGULOS CUALESQUIERA

Para resolver un triángulo cualquiera, tenemos en cuenta las siguientes relaciones entre sus elementos:

- La suma de sus ángulos 180 grados

- El teorema del seno

- El teorema del coseno

También para saber si un triángulo rectángulo lo podemos saber gracias al Teorema de Pitágoras.

Un triángulo cualquiera queda determinado cuando conocemos, como mínimo, tres de sus elementos, excepto en el caso de los tres ángulos.

Para resolver un triángulo pueden observarse 3 casos:

1-CONOCER LOS 3  LADOS

Y ahora se resolvería este triángulo:

2- Y también podemos conocer 2 lados y ángulo o 1 lado y 2  ángulos

EXPRESIONES DEL ÁREA DE UN TRIÁNGULO

El área de un triángulo puede calcularse mediante el producto de un medio po un lado, por el otro lado y por el seno del ángulo comprendido entre ambos lados.

Fórmulas:  

Ahora vamos a ver las opciones de los distintos triángulos a ver si siempre se puede hallar el área con la misma fórmula... 

- TRIÁNGULO RECTÁNGULO: 

-TRIÁNGULO ACUNTÁNGULO:

-TRIÁNGULO OBTUSÁNGULO: 

En conclusión; Funciona siempre la misma fórmula

La fórmula de Herón:

Herón quería cambiar sen A y decía que el área del triángulo depende de los 3 lados; y esta fórmula se basa en dos teoremas:

Ahora os voy a mostrar la DEMOTRACIÓN de este teorema:

TEOREMA DEL COSENO

 Se trata de un teorema de la trigonométria que en cada triángulo indica que el cuadrado de la longitud de cada lado guarda una relación con los cuadrados de los lados restantes y el ángulos que estos comprenden.

Demostración de este teorema:

¿PARA QUE SE UTILIZA ESTE TEOREMA?

- Cálculo de un ángulo de un triángulo del que son conocidos sus tres lados.

- Cálculo de un lado del triángulo conocidos los otros dos y el ámgulo comprendido entre ellos.

TEOREMA DEL SENO

Este teorema afirma que, en un triángulo cualquiera, los lados son proporcionales a los senos de sus triángulos opuestos.

Demostración de este teorema: 

¿PARA QUE SE UTILIZA EL TEOREMA DEL SENO?

- Para el cálculo del lado de un triángulo, conocido su ángulo opuesto, otro lado y su ángulo opuesto.

- Para el cálculo de un ángulo, conocido se lado opuesto, otro ángulo y su lado opuesto.

RELACIONES ENTRE LAS RAZONES TRIGONOMÉTRICAS DE CUALQUIER ÁNGULO.

RAZONES TRIGONOMÉTRICAS DE UN ÁNGULO CUALQUIERA.

Circunferencia goniométrica: es una circunferencia de radio una unidad de longitud y centrada en el origen de las coordenadas de un sistema de referencia de coordenadas cartesianas.

El Signo de las razones trigonométricas: del seno y del coseno en cada uno de los cuadrantes viene dado por el singo que tengan las ordenadas y las abscisas.

Ahora os vamos a mostrar la tabla de las razones trigonométricas de varios ángulos: